THỨ HÌNH HỌC KHÔNG BAO HÀM CÁC SỐ ĐO (tiếp theo)

Trong bài viết trước, ta đã hoàn thiện các công cụ cần thiết cho những tư duy và lý luận mà ta sẽ thực hiện. Ta đã biết rằng Trái Đất là một đa tạp hai chiều có thể định hướng, hữu hạn và không có biên, câu hỏi bây giờ là từ những tính chất trên ta đã có thể xác định hình dáng của Trái Đất hay chưa? Giả sử ta đang sống trên một thế giới mà ta đã có trong tay một cuốn sách gồm tất cả các bản đồ vẽ mọi địa điểm của nó, nếu ta cố gắng cắt bỏ đi các phần trùng nhau, uốn nắn và lắp ráp chúng lại, chúng ta có thể thu được các kết quả khả dĩ nào về hình dạng của thế giới?

Hình ảnh sau đây cho ta một ví dụ về một dạng hình học khả dĩ của Trái Đất.

Nếu những nhà du hành mà Trái Đất của họ có hình dạng như này, câu chuyện của họ cũng sẽ không khác chúng ta là mấy. Họ chẳng bao giờ đi ra khỏi Trái Đất, bởi vì một hình xuyến hai lỗ cũng không có biên nào hết. Họ cũng có thể vẽ bản đồ bất cứ khu vực nào trên Trái Đất này rồi tập hợp chúng lại với nhau thành một atlas. Liệu các nhà địa lí có thể chỉ dựa vào việc nghiên cứu atlas này mà xác định được dạng đa tạp họ đang sống hay không? Hiển nhiên rằng các công dân trên thế giới đó không hề nhận ra Trái Đất của họ có bất kì cái lỗ nào bởi vì các miền trên đó đều liên thông với nhau.

Như vậy, ta đã biết rằng hình cầu, cũng như hình xuyến không phải là các khả năng duy nhất của Trái Đất. Bây giờ, liệu ta có thể liệt kê được tất cả các dạng hình học có thể có của Trái Đất hay không? Cụ thể hơn, liệu ta có sẵn một danh sách đầy đủ các đa tạp hai chiều có thể định hướng, hữu hạn và không có biên, trước khi một đột phá nào đó chỉ ra rõ ràng rằng Trái Đất phải có hình dạng như thế nào hay không? Câu trả lời, cùng với chứng minh của nó, là một thành tựu vĩ đại của thế kỉ XIX. Câu trả lời, nằm trong phạm vi định lý phân loại các đa tạp hai chiều, thực ra khá đơn giản, nếu ta đã trình bày về hình xuyến hai lỗ, ta cũng có thể nghĩ về một hình xuyến ba lỗ, năm lỗ, bảy lỗ, hay thậm chí với số lỗ bất kì. Tất cả chúng đều không đồng phôi, đều thỏa mãn tất cả các điều kiện mà các đa tạp hai chiều có thể định hướng phải thỏa mãn, chúng đều là các hình mẫu khả dĩ cho Trái Đất. Và quan trọng nhất, đó là tất cả, tập hợp các hình xuyến trên đã là một danh sách đầy đủ.

Chúng ta đang đi đến những bước cuối cùng của mạch suy nghĩ. Để tổng kết lại, ta biết rằng Trái Đất là một đa tạp hai chiều hữu hạn không biên và có thể định hướng, từ đó mà ta có được một danh sách đầy đủ các hình dạng của Trái Đất là tập hợp các hình xuyến với số lỗ bất kì và hình cầu. Câu hỏi cuối cùng còn lại là làm sao để từ việc có trong tay một atlas của Trái Đất, ta có thể chỉ rõ ràng rằng Trái Đất có hình dáng như thế nào. Bạn có thể thử, một lần nữa, ghép các bản đồ lại với nhau, tuy nhiên làm như vậy đòi hỏi các kĩ thuật rất phức tạp, ví dụ như với hình xuyến ba lỗ ở trên, và trong trường hợp tổng quát làm như vậy đôi khi không dẫn đến kết quả. Câu hỏi này làm nảy sinh các hướng mới trong việc xem xét sự đồng phôi giữa các đa tạp, một trong số đó, rất thú vị, là quan sát các đường khép kín hay vòng lặp trên các đa tạp. Đây là những quỹ đạo được vẽ ra trên bề mặt, bắt đầu và kết thúc tại cùng một điểm. Bạn có thể tưởng tượng đó là hình ảnh vẽ nên bởi sợi dây mà mình mang theo sau khi thực hiện chuyến du hành vòng quanh Trái Đất. Các vòng lặp được phân biệt với nhau bởi các mối quan hệ gọi là đồng điều. Đa tạp khác nhau về mặt topo có thể được phân loại thông qua tính chất của các vòng lặp của chúng. Sẽ là quá xa khi ta tiếp tục đi sâu thêm về phương diện này, nhưng có một trường hợp đặc biệt quan trọng với chúng ta sẽ được đề cập đến.

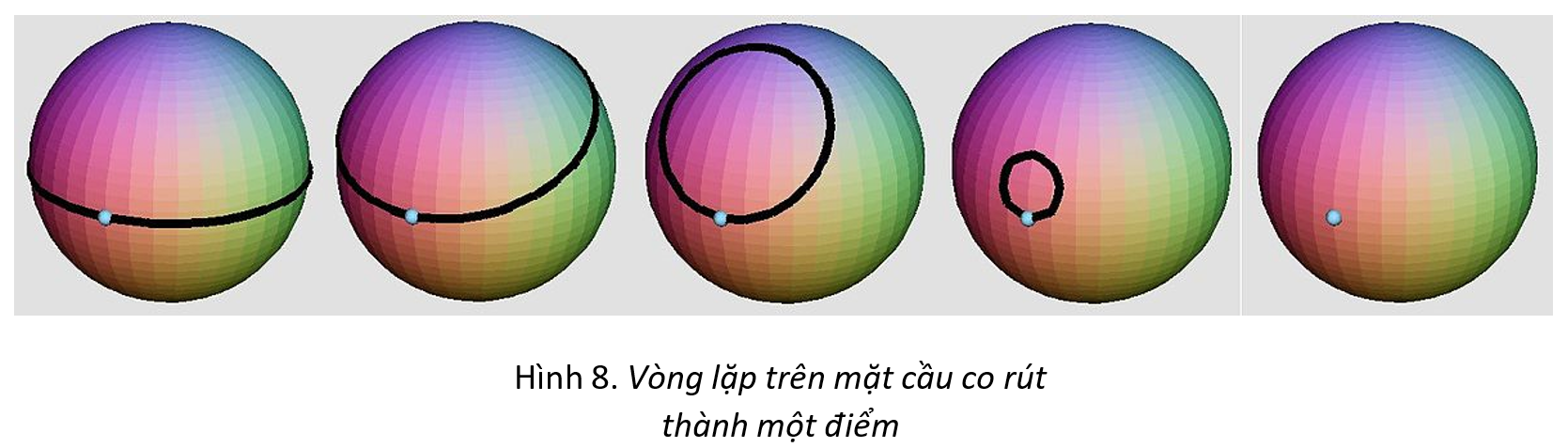
Hãy tưởng tượng rằng khi Magellan du hành quanh Trái Đất, thủy thủ đoàn của ông mang theo một sợi dây mà ta giả sử có chiều dài rất lớn. Một đầu của sợi dây được neo vào bến tàu nơi họ xuất phát, trong suốt quá trình tàu đi, họ thả sợi dây để nó ghi lại quỹ đạo của chuyến hành trình. Họ tiếp túc đi để hoàn thành chuyến du hành, khi họ quay được về đến điểm xuất phát sau khi đã để lại trên bề mặt Trái Đất một vòng dây khổng lồ, cột hai đầu của sợi dây lại với nhau, ta có hình ảnh của một vòng lặp trên đa tạp hai chiều mà ta đang sống. Bây giờ việc ta cần làm là kéo sợi dây về phía mình, đúng vậy, kéo nó, bằng bất cứ cách nào cũng được, miễn sao cho vòng dây không nhảy lên khỏi bề mặt hay là chui xuống đất. Câu hỏi là liệu ta có thể kéo sợi dây được về vị trí xuất phát ban đầu hay không? Nếu là trên một mặt phẳng hay một mặt cầu, câu trả lời hiến nhiên là có. Thậm chí nếu đó có là một vòng dây lớn vòng quanh xích đạo, nếu ta kéo nó về phía mình, nó có thể, chẳng hạn trượt về phía Bắc, lên đến Bắc Băng Dương, tới điểm cực Bắc, sau đó trượt xuống Moscow, đi qua Trung Quốc và cuối cùng ta sẽ thu lại được toàn bộ sợi dây. Khi di chuyển, hình ảnh của sợi dây tạo thành một chuỗi các vòng càng lúc càng nhỏ dần cho đến khi trở thành một điểm khi quay về với chúng ta (xem hình 8). Nếu mặt cầu không tròn một cách tuyệt đối, như quả lê mà Columbus đã tưởng tượng, mặc dù đôi khi sẽ phải có nhiều dây hơn, ta vẫn có thể kéo sợi dây thành một điểm theo cách tương tự.

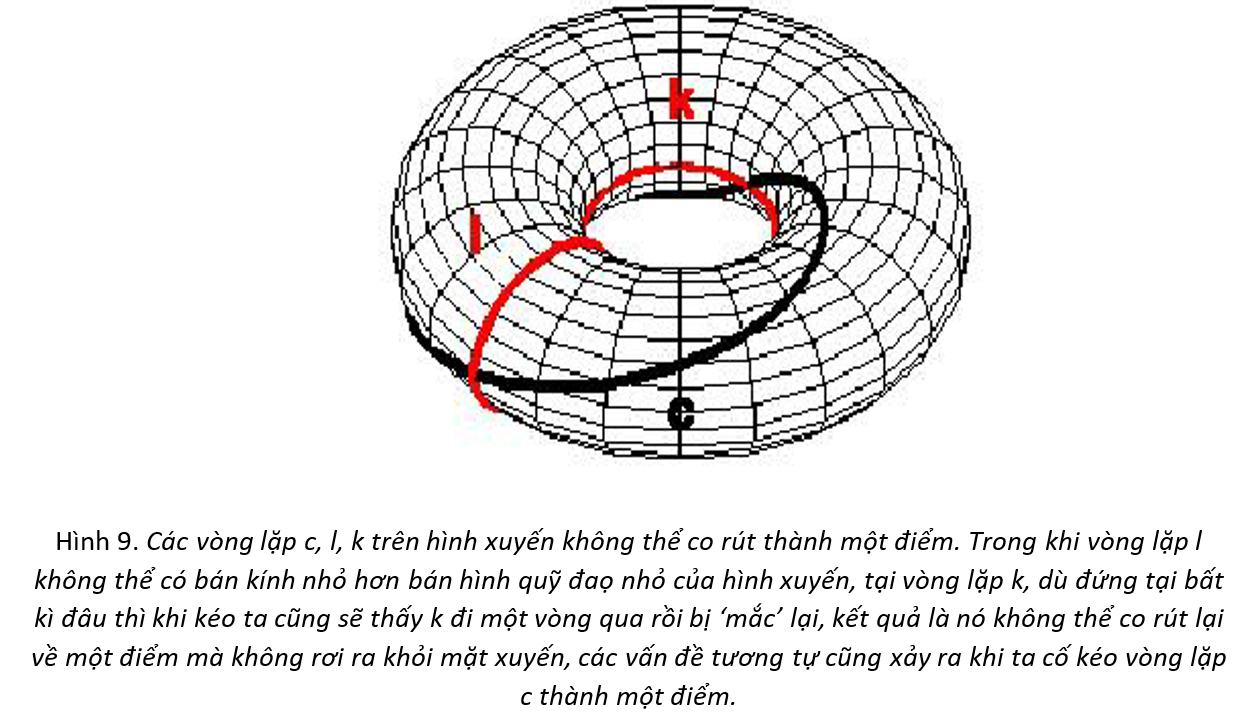
Có thể bạn đã nhận ra, tồn tại những vòng lặp trên các hình xuyến không thể co rút thành một điểm dù ta có cố kéo theo cách nào. Nếu ta đi vòng quanh một cái lỗ, ta thậm chí còn không thể kéo nó nhỏ hơn đường kính của cái lỗ đó. Điều tương tự cũng diễn ra trên hình xuyến với số lỗ bất kì.

Một đa tạp có tính chất mà tất cả vòng lặp trên đó có thể co rút trở thành một điểm duy nhất được gọi là các đa tạp đơn liên. Dựa vào định lý phân loại các đa tạp hai chiều, ta có thể chỉ ra rằng mặt cầu và các đồng phôi của nó là các đa tạp hai chiều đơn liên duy nhất. Như vậy, câu trả lời cho câu hỏi của chúng ta đặt ra ngay từ đầu đã ngã ngũ. Mặc dù nhìn chung là khó, tuy nhiên các nhà địa lí sống trên một bề mặt có thể thông qua việc nghiên cứu atlas của bề mặt đó và xác định xem đa tạp mà nó biểu diễn có đơn liên hay không, từ đó mà khẳng định được đó có phải là mặt cầu hay không. Đối với riêng chúng ta, có thể khẳng định rằng, không cần thêm chiều thứ ba, những con người trên Trái Đất vẫn có cách xác định hành tinh mà chúng ta đang sinh sống có dạng hình cầu.

BƯỚC RA NGOÀI TRÁI ĐẤT

Người đọc lưu tâm có thể chú ý tới vài điểm sau đây mà bài viết đã phần nào cố tình không đề cập đến.

Thứ nhất, các phát biểu toán học trong bài viết không có vẻ toán học lắm, nó chỉ trình bày kết quả mà thiếu khuyết các phần chứng minh hay lập luận, ví dụ như vì sao các mặt xuyến với số lỗ khác nhau là không đồng phôi, và cũng không đồng phôi với mặt cầu, hay như cụ thể một quá trình co rút của vòng lặp là gì. Các kết quả trên là rất đẹp tuy nhiên lề giấy là quá nhỏ để viết một chứng minh đầy đủ cho chúng. Bạn đọc quan tâm có thể tìm hiểu thêm về topo học, một bộ môn mà người viết cho rằng vẻ đẹp của nó có thể sánh ngang với các vì sao trên bầu trời đêm.

Thứ hai, bài viết chỉ để cập đến sự giống nhau trên quan niệm đồng phôi, một quan niệm không chuẩn về sự giống nhau trong cách nhìn nhận thông thường, trong khi đó hình dạng thực sự của Trái Đất trên quan điểm hình học còn bị bỏ ngõ. Quan điểm của Columbus nhìn nhận Trái Đất có hình dạng như một quả lê là do các lâp luận sai, có thể dễ dàng bác bỏ bằng một vài phép đo ở các vùng cực. Tuy nhiên một khẳng định mạnh cụ thể là khó khăn hơn rất nhiều, mà về lý thuyết ta phải thực hiện vô số phép đo trên bề mặt Trái Đất. Trên thực tế Trái Đất cũng không phải có hình cầu hoàn hảo mà nhìn chung hơi phẳng hơn một chút ở hai cực. Tuy nhiên, không có gì là ngăn cản chúng ta đặt giả thuyết điều gì sẽ xảy ra khi ta có các đo đạc mình cần. Câu trả lời được trình bày bởi Rieman năm 1854 trước sự chứng kiến của nhà bác học vĩ đại Carl Friedrich Gauss, một câu chuyện thú vị có thể được đề cập lại sau.

Cuối cùng, như nhiều lần đề cập về hình dáng của vũ trụ, thực ra bài viết này chỉ là bước đệm cho một cái nhìn toàn cục hơn về bức tranh hình khối của vũ trụ, nơi mà ở đó các kĩ thuật ta sử dụng ở đây trở nên quan trọng hơn rất nhiều khi mà ta thực sự có rất ít thông tin về vũ trụ cũng như không thể thực sự thoát ra khỏi đó. Bài toán như một giả thuyết cho dạng hình học của vũ trụ là một hệ quả của một trong những vấn đề lớn nhất mọi thời đại của toán học nói riêng và khoa học nói chung, một giả thuyết được mở đầu bởi một người Pháp và kết thúc bởi một người Nga, giả thuyết Poincaré. Đó cũng sẽ là chủ đề mà ta sẽ gặp lại trong những bài viết sau.

Trần Minh Thông

Ban nội dung CLB Thiên văn USAC