THỨ HÌNH HỌC KHÔNG BAO HÀM CÁC SỐ ĐO

Trong bài viết trước, ta đã chu du qua dòng lịch sử dài của câu chuyện về hình dáng của Trái Đất. Phần tiếp theo trình bày thuộc một trong những lĩnh vực có thể gây ám ảnh với nhiều người – toán học. Tuy nhiên, như bạn sẽ thấy sau đây, hoàn toàn không tồn tại các công thức và tính toán đáng sợ, việc bạn cần chỉ là để trí tưởng tượng của mình bay xa ngoài hiện thực một chút bởi bài viết sẽ đề cập một trong những lĩnh vực mỹ miều nhất của toán học, topo học (topology). Sở dĩ ta phải nhắc đến toán bởi vì một suy luận như những sinh vật từ một không gian ít chiều nhìn lên không gian nhiều chiều hơn không thể thực hiện được bằng kinh nghiệm thông thường mà chỉ có thể nhận được thông qua các lý luận hình thức. Ngoài ra, độ chính xác tuyệt đối trong các suy luận toán học cũng là điều mà ta hướng tới.

Đầu tiên, ta cần chính xác hóa các khái niệm mà ta sẽ sử dụng bằng cách định nghĩa lại chúng một cách mạch lạc để dẫn đường cho những suy nghĩ.

Thứ nhất, về các bề mặt, đây là khái niệm quan trọng nhất với chúng ta, nó mô tả cho các thế giới khả dĩ mà ta đang sống, tức là ta sẽ xem xét Trái Đất thông qua bề mặt của nó mà không cần thiết quan tâm tới các lớp đất đá và magma phía dưới. Bề mặt, mà để chính xác hóa ta gọi là đa tạp hai chiều, là đối tượng mà mọi khu vực trên đó đều có thể vẽ được thành một bản đồ nào đó trên một tờ giấy. Một mặt phẳng hay tờ giấy nghiễm nhiên là đa tạp hai chiều, mặt cầu tương tự cũng là đa tạp hai chiều. Khái niệm hai chiều ở đây có nghĩa là với mỗi điểm trên đối tượng thì các điểm xung quanh nó có thể biểu diễn được chỉ bằng hai hướng độc lập, điều này dẫn đến ta có thể xác định mỗi liên hệ giữa các điểm và vẽ được bản đồ trên một tờ giấy. Lưu ý rằng, chiều ở đây không phải như cách chúng ta thường mường tượng là không gian cần để ta đặt vật

thể vào đó mà chỉ số chiều mà một sinh vật sống trên đó cảm nhận bằng kinh nghiệm. Nói thêm một chút về các đa tạp hai chiều, nếu bạn có thể tập hợp lại đầy đủ tất cả các bản đồ vẽ các khu vực của một bề mặt, ta sẽ có đươc một atlas (như các atlas Việt Nam hay thế giới), một atlas khi đó được coi là biểu diễn của một đa tạp hai chiều. Bạn có thể thấy các bề mặt, hay đa tạp hai chiều như cách định nghĩa của chúng ta cho phép làm xuất hiện các đối tượng kỳ dị. Hãy nghĩ về một dải Mobius như trong hình 4, một đối tượng như vậy là bề mặt theo nghĩa của chúng ta nhưng không thể là bề mặt của bất kì vật rắn thực sự nào trong thế giới ta đang sống.

Không phải lúc nào ta cũng có thể định nghĩa được phía nào là bên phải và phía nào là bên trái trên một đa tạp hai chiều, dải Mobius trên cũng cho ta một ví dụ về điều đó, thử vẽ một mũi tên hai chiều trên đó và đánh dấu bên nào là bên phải và trái, nếu ta trượt mũi tên đi đến khi nó trở về vị trí ban đầu, bạn sẽ thấy hai chiều mà ta đánh dấu đã bị đảo ngược. Tuy nhiên, với những bề mặt mà ta có thể định nghĩa trái và phải trên đó thì đó là bề mặt của một vật thể, và ngược lại. Một bề mặt như vậy, cái được gọi là đa tạp có thể định hướng, là những đối tượng mà ở đây ta tập trung xem xét.

Thứ hai, ta trình bày hai thuật ngữ mà đôi khi gây nhầm lẫn trong thực tế. Đầu tiên là biên, biên của một đa tạp hai chiều là tập hợp các lề của nó theo quan sát của sinh vật sống trên đó, tức là những địa điểm mà có thể “bước đi” ra khỏi đa tạp đó. Các đa tạp hai chiều có thể có biên hoặc không, mặt phẳng không có biên, hình tròn thì có, đó là đường tròn bao bên ngoài nó. Chú ý thêm rằng nếu một đa tạp có biên thì số chiều của biên sẽ ít hơn số chiều của bản thân nó. Thuật ngữ thứ hai là hữu hạn, một đa tạp hai chiều là hữu hạn, hay để chính xác ta gọi là compact, nếu ta có thể phủ nó bằng hữu hạn các bản đồ có kích thước nhất định bất kỳ. Tương tự như trên, một hình tròn là hữu hạn, còn mặt phẳng thì không. Tuy nhiên, cho rằng hai khái niệm trên tương đương là một sai lầm cố hữu. Một sự suy luận rằng vật thể là vô hạn bởi vì ta không thể tìm ra bất kì biên nào của nó có thể trở nên sai lầm chết người. Hãy xem xét trường hợp của một mặt cầu và một mặt xuyến, chúng vừa hữu hạn vì có kích thước hữu hạn nhưng bạn cũng không thể tìm bất kì biên nào của chúng.

Tới đây, bằng kinh nghiệm ta có thể rút ra kết luận rằng (bề mặt) Trái Đất là một đa tạp hai chiều có thể định hướng, hữu hạn bởi cách vẽ bản đồ của Ptolemy, và không có biên.

Thứ ba, thế nào là giống nhau? Đây là một điều quan trọng, ta phải chỉ rõ sự giống nhau mà ta hướng tới nghĩa là gì, bởi có nhiều cách nhìn về vấn đề này tùy vào bạn muốn xem xét khía cạnh nào. Khi nhắc đến hình dạng, ta thường coi các quả bóng là giống nhau, đều có hình cầu, tức là ta không quan tâm đến kích thước của chúng, tương tự với những chiếc bánh donut. Trong bài viết này, ta gọi hai đa tạp hai chiều là giống nhau, hoặc đồng phôi, nếu ta có một phép tương ứng sao cho mỗi điểm thuộc đa tạp hai chiều này ứng với một và chỉ một điểm thuộc đa tạp hai chiều kia, trong đó phép tương ứng phải đảm bảo tính liên tục, nghĩa là nếu điểm A qua phép tương ứng trở thành điểm B, thì các điểm ở gần A cũng tương ứng trở thành các điểm ở gần B. Một cách sinh động hơn, nếu hai hình là đồng phôi, thì chúng chia sẻ chung một atlas, khi ta sắp xếp lại các bản đồ của một hình, cắt bỏ đi các phần bị trùng và dán chúng lại với nhau, thì ta hoàn toàn có thể thu được các hình đồng phôi với nó . Bạn có thể dễ dàng nhận ra rằng khai niệm giống nhau này hơi khác với những gì ta thường nhìn nhận trong hình học. Điều này cho phép điều kỳ lạ diễn ra, các hình sau trong hình 5 được coi là giống nhau. Trong khi đó, mặt cầu và mặt xuyến là không đồng phôi.

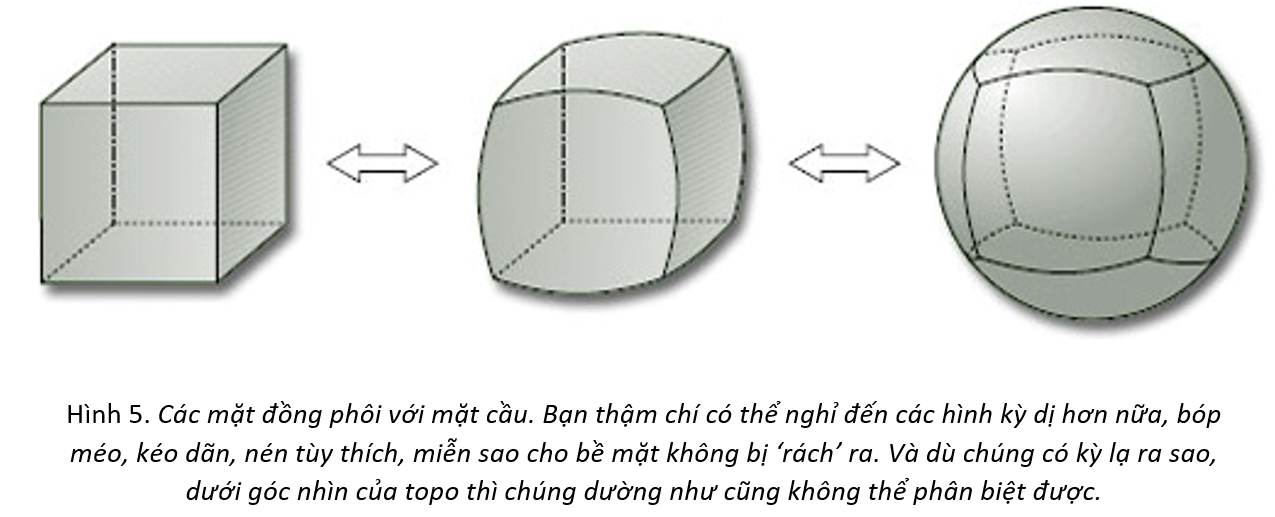
Những điều kỳ dị như vậy xuất hiện là do đặc tính của môn topo học, nơi mà ta chỉ xem xét đến những bản chất căn bản nhất của các hình dạng. Cụ thể hơn, topo khác với hình học ở chỗ nó không quan tâm tới góc hay độ dài, hai bề mặt bất kì trở nên giống nhau khi bạn có thể kéo dãn hoặc nén một hình lại thành hình kia miễn sao phép biến đổi không làm xé rách hình (bởi vì như vậy sẽ làm mất đi tính liên tục). Như vậy, câu hỏi của Columbus bỗng trở nên vô nghĩa trong phạm vi của môn topo. Bạn sẽ tự hỏi tại sao ta lại cần những tính chất nghe có vẻ siêu hình như vậy, thú thật đôi khi các nhà toán học làm việc mà không quan tâm đến các ứng dụng của nó, đơn thuần bởi vì vẻ đẹp. Tuy nhiên trong trường hợp của chúng ta những lý luận như vậy là cần thiết bởi vì ta không cho phép mình bước ra khỏi bề mặt Trái Đất mà chỉ có thể thực hiện những phép đo trên bề mặt, và việc sắp xếp các bản đồ với nhau xem ra là dễ hơn rất nhiều với việc đo tất cả tam giác có thể vẽ ra trên bề mặt Trái Đất, ngoài ra những suy nghĩ đi xa thực tế vật lý kiểu này, như đã nói, đôi khi có thể dẫn ta đến những phát hiện mới quan trọng như vấn đề về hình dáng của vũ trụ. Trong bài viết sau, ta sẽ tiếp tục câu chuyện còn dang dở về các thế giới khả dĩ, và vẽ những nét mực đầu tiên cho bức tranh về toàn cảnh thứ lớn lao bao trùm tất cả ngoài kia.

Trần Minh Thông

Ban nội dung CLB Thiên văn USAC